Examples¶
This page illustrates the usage of the PyMacroFin library with two examples. For details on model attributes, methods, and options used in these examples, please see the appropriate documentation pages.
One Dimensional Problem¶
We replicate the log-utility results from Brunnermeier and Sannikov (2014) [1] using the PyMacroFin package. For model algebra, please see the cited paper. The code is presented here.
from PyMacroFin.model import macro_model
import numpy as np
import pandas as pd
import time
import PyMacroFin.utilities as util
from PyMacroFin.system import system
# initial guess function for endogenous variables
def init_fcn(e,c):
if e<.3:
q = 1.05+.06/.3*e
psi = 1/.3*e
sigq = -.1*(e-.3)**2+.008
else:
psi = 1
sigq = 0
q = 1.1 - .03/.7*e
return [q,psi]
# boundary condition function for eta == 0
def eta_minimum(d):
psi = 0
q = (2*d['ah']*d['kappa']+(d['kappa']*d['r'])**2.+1)**0.5 - d['kappa']*d['r']
return [q,psi]
def define_model(npoints):
m = macro_model(name='BruSan14_log_utility')
m.set_endog(['q','psi'],init=[1.05,0.5])
m.prices = ['q']
m.set_state(['e'])
m.params.add_parameter('sig',.1)
m.params.add_parameter('deltae',.05)
m.params.add_parameter('deltah',.05)
m.params.add_parameter('rho',.06)
m.params.add_parameter('r',.05)
m.params.add_parameter('ae',.11)
m.params.add_parameter('ah',.07)
m.params.add_parameter('kappa',2)
m.equation('iota = (q**2-1)/(2*kappa)')
m.equation('phi = 1/kappa*((1+2*kappa*iota)**0.5-1)')
m.equation('sigq = (((ae-ah)/q+deltah-deltae)/(psi/e-(1-psi)/(1-e)))**0.5 - sig',plot=True,latex=r'$\sigma^q$')
m.equation('sige = (psi-e)/e*(sig+sigq)')
m.equation('mue = sige**2 + (ae-iota)/q + (1-psi)*(deltah-deltae)-rho')
m.equation('er = psi/e*(sig+sigq)**2',plot=True,latex=r'$E[dr_t^k-dr_t]/dt$')
m.equation('sigee = sige*e',plot=True,latex=r'$\sigma^{\eta} \eta$')
m.equation('muee = mue*e',plot=True,latex=r'$\mu^{\eta} \eta$')
m.endog_equation('q*(r*(1-e)+rho*e) - psi*ae - (1-psi)*ah + iota')
m.endog_equation('(psi-e)*d(q,e) - q*(1-sig/(sig+sigq))')
m.hjb_equation('mu','e','mue')
m.hjb_equation('sig','e','sige')
m.constraint('psi','<=',1,label='upper_psi')
m.constraint('psi','>=',0,label='lower_psi')
m.boundary_condition({'e':'min'},eta_minimum)
s = system(['upper_psi'],m)
s.equation('sigq = sig/(1-(psi-e)*d(q,e)/q) - sig')
s.endog_equation('1 - psi')
s.endog_equation('q*(r*(1-e)+rho*e) - ae + iota')
m.systems.append(s)
m.options.ignore_HJB_loop = True
m.options.import_guess = False
m.options.guess_function = init_fcn
m.options.inner_plot = False
m.options.outer_plot = False
m.options.final_plot = True
m.options.n0 = npoints
m.options.start0 = 0.0
m.options.end0 = 0.95
m.options.inner_solver = 'least_squares'
m.options.derivative_plotting = [('q','e')]
m.options.min_iter_outer_static = 5
m.options.min_iter_inner_static = 0
m.options.max_iter_outer_static = 50
m.options.return_solution = True
m.options.save_solution = False
m.options.price_derivative_method = 'backward'
return m
if __name__=='__main__':
npoints = 100
tic = time.time()
m = define_model(npoints)
df = m.run()
toc = time.time()
print('elapsed time: {}'.format(toc-tic))
The results are as follows:
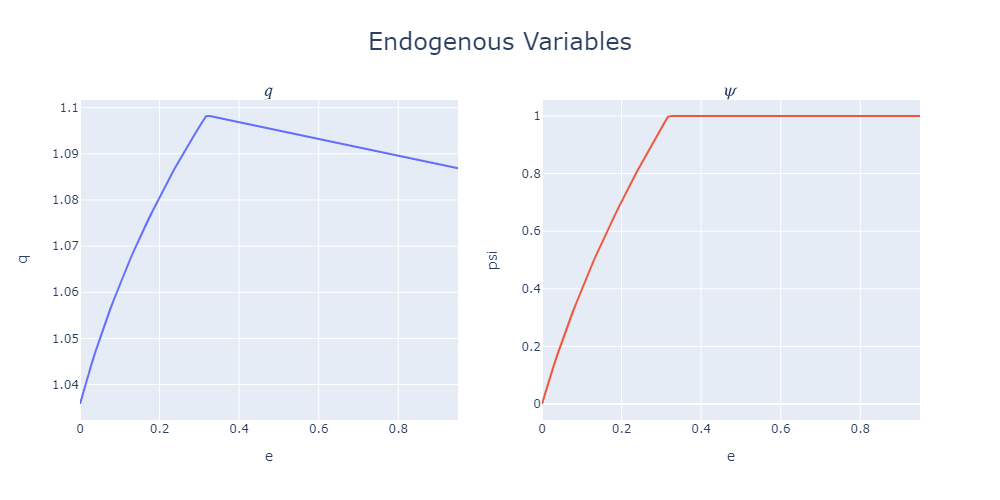
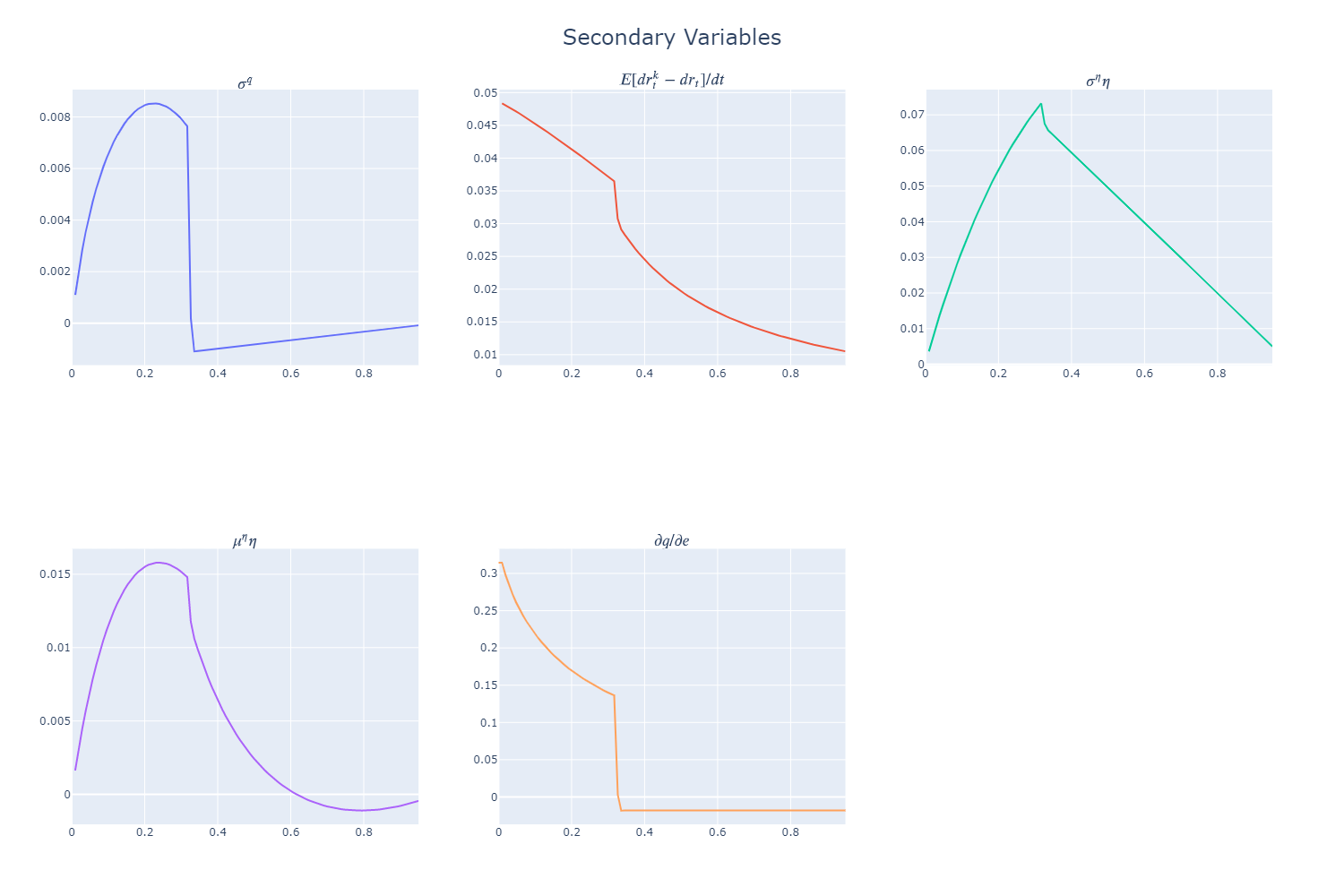
Two Dimensional Problem¶
An extension of Brunnermeier and Sannikov (2014) [1] with two agents and time-varying aggregate volatility
is used as the two-dimensional example problem. This document outlines the
model algebra and contains the code in an appendix, which is also provided here.
from PyMacroFin.model import macro_model
import numpy as np
import pandas as pd
import time
import PyMacroFin.utilities as util
def define_model():
m = macro_model(name='BruSan')
m.set_endog(['q','psi','mue','sigqk','sigqs'],init=[1,0.95,0,0,0],
latex=[r'$q$',r'$\psi$',r'$\mu^{\eta}$',
r'$\sigma^{q,k}$',r'$\sigma^{q,\sigma}$'])
m.prices = ['q']
m.set_state(['e','z'])
m.set_value(['vi','vh'],init=[0.04,0.04],latex=[r'$\xi^i$',r'$\xi^h$'])
m.params.add_parameter('gammai',2)
m.params.add_parameter('gammah',3)
m.params.add_parameter('ai',.1)
m.params.add_parameter('ah',.1)
m.params.add_parameter('rhoi',.04)
m.params.add_parameter('rhoh',.04)
m.params.add_parameter('sigz',.01)
m.params.add_parameter('sigbar',.5)
m.params.add_parameter('deltai',.04)
m.params.add_parameter('deltah',.04)
m.params.add_parameter('kappa_p',2)
m.params.add_parameter('kappa_z',5)
m.params.add_parameter('zetai',1.15)
m.params.add_parameter('zetah',1.15)
m.params.add_parameter('kappa_l',.9)
m.params.add_parameter('ebar',0.5)
m.equation("sigma = z")
m.equation("wi = psi/e")
m.equation("wh = (1-psi)/(1-e)")
m.equation("ci = vi**((1-zetai)/(1-gammai))")
m.equation("ch = vh**((1-zetah)/(1-gammah))")
m.equation("iotai = (q-1)/kappa_p")
m.equation("iotah = (q-1)/kappa_p")
m.equation("phii = log(1+kappa_p*iotai)/kappa_p-deltai")
m.equation("phih = log(1+kappa_p*iotah)/kappa_p-deltah")
m.equation("muz = kappa_z*(sigbar-sigma)")
m.equation("muk = psi*phii+(1-psi)*phih")
m.equation("signis = wi*sigqs")
m.equation("signhs = wh*sigqs")
m.equation("signik = wi*(sigqk+sigma)")
m.equation("signhk = wh*(sigqk+sigma)")
m.equation("siges = e*(1-e)*(signis -sigqs)")
m.equation("sigek = e*(1-e)*(signik - (sigqk+sigma))")
m.equation("sigxik = d(vi,e)/vi*sigek*e")
m.equation("sigxhk = d(vh,e)/vh*sigek*e")
m.equation("sigxis = d(vi,e)/vi*siges*e + d(vi,z)/vi*sigz*z")
m.equation("sigxhs = d(vh,e)/vh*siges*e + d(vh,z)/vh*sigz*z")
m.equation("muq = d(q,e)/q*mue*e + d(q,z)/q*muz*z + \
1/2*d(q,e,e)/q*((siges*e)**2 + (sigek*e)**2) + \
1/2*d(q,z,z)/q*(sigz*z)**2 + d(q,e,z)/q*siges*e*sigz*z")
m.equation("muri = (ai-iotai)/q + phii + muq + sigma*sigqk")
m.equation("murh = (ah-iotah)/q + phih + muq + sigma*sigqk")
m.equation("r = muri - gammai*wi*((sigqs**2)+(sigma+sigqk)**2) + \
sigqs*sigxis + (sigqk+sigma)*sigxik")
m.equation("muni = r + wi*(muri-r)-ci")
m.equation("munh = r + wh*(murh-r)-ch")
m.endog_equation("kappa_l/e*(ebar-e)+(1-e)*(muni - muk - muq\
- sigma*sigqk + (sigqk+sigma)**2 + sigqs**2 \
- wi*sigqs**2 - wi*(sigqk+sigma)**2) - mue")
m.endog_equation("(ci*e+ch*(1-e))*q - psi*(ai-iotai) - (1-psi)*(ah-iotah)")
m.endog_equation("muri - murh + gammah*wh*((sigqs**2)+(sigqk+sigma)**2) - \
gammai*wi*((sigqs)**2+(sigqk+sigma)**2) + sigqs*sigxis + \
(sigqk+sigma)*sigxik - sigqs*sigxhs - (sigqk+sigma)*sigxhk")
m.endog_equation("(sigz*z*d(q,z) + siges*e*d(q,e))-sigqs*q")
m.endog_equation("sigek*e*d(q,e) - sigqk*q")
m.hjb_equation('mu','e','mue*e')
m.hjb_equation('mu','z','muz*z')
m.hjb_equation('sig','e',"(siges*e)**2 + (sigek*e)**2")
m.hjb_equation('sig','z',"(sigz*z)**2")
m.hjb_equation('sig','cross',"siges*e*sigz*z")
m.hjb_equation('u','vi',0)
m.hjb_equation('u','vh',0)
m.hjb_equation('r','vi',"-1*(1-gammai)*(1/(1-1/zetai)*(ci-(rhoi+kappa_l))\
+r-ci+gammai/2*(wi*(sigqs)**2 +wi*(sigqk+sigma)**2))")
m.hjb_equation('r','vh',"-1*(1-gammah)*(1/(1-1/zetah)*(ch-(rhoh+kappa_l))\
+r-ch+gammah/2*(wh*(sigqs)**2 +wh*(sigqk+sigma)**2))")
m.options.loop = False
m.options.outer_plot = True
m.options.n0 = 50
m.options.n1 = 50
m.options.start0 = 0.05
m.options.start1 = 0.05
m.options.end0 = 0.95
m.options.end1 = 0.95
m.options.inner_solver = 'newton-raphson'
m.options.parallel = True
return m
if __name__=='__main__':
tic = time.time()
m = define_model()
util.deploy_dash(m)
m.run()
toc = time.time()
print('elapsed time: {}'.format(toc-tic))
The results are as follows (note that when running the visualization application the plots are fully interactive as opposed to this static image):
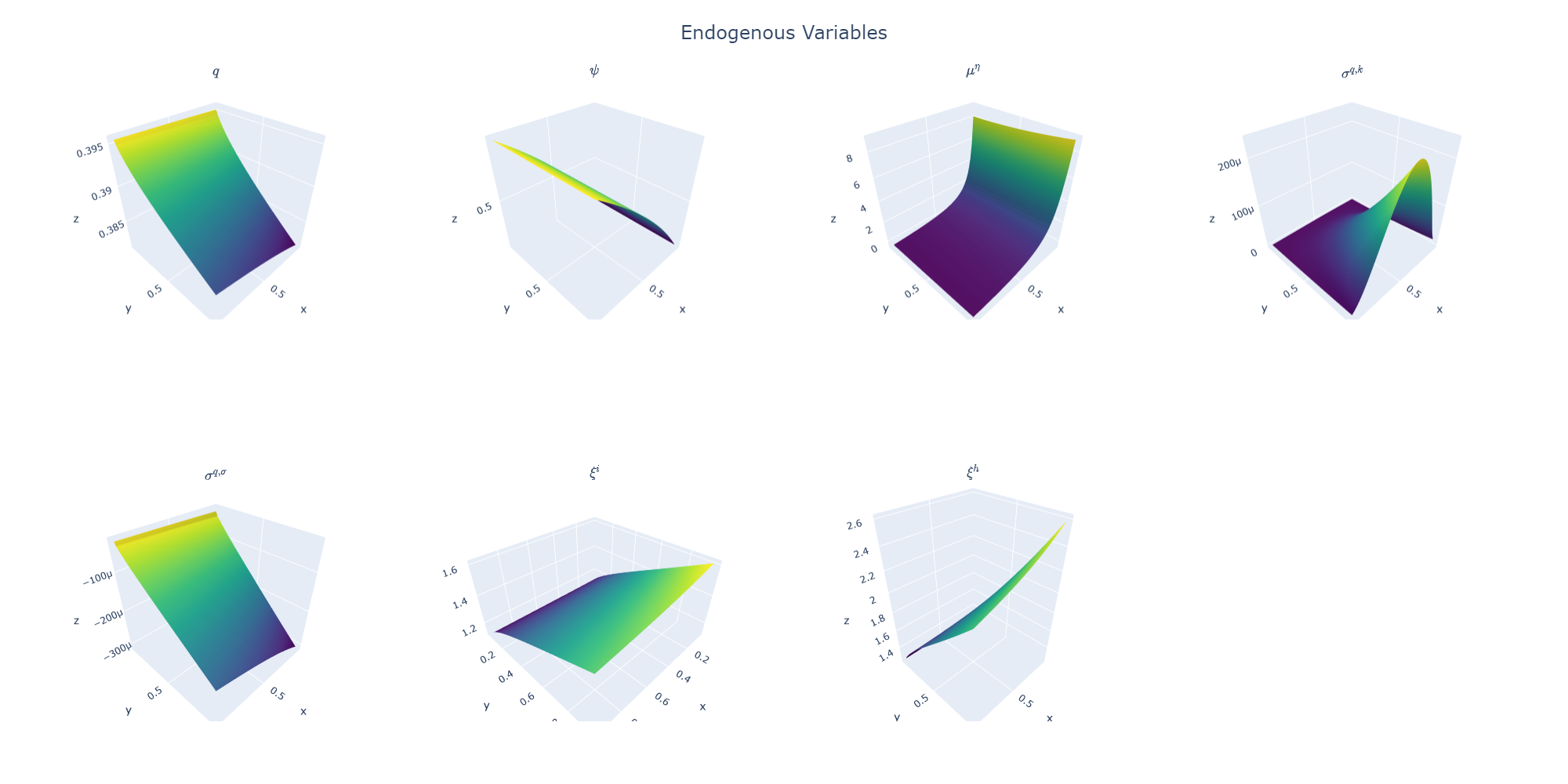
Footnotes
| [1] | (1, 2)
|